Le fonctionnement du DES
Histoire
Jusqu'à la moitié du XXe siècle, une multitude de chiffres, plus ou moins efficaces, se font concurrence pour assurer la confidentialité des messages transitant, de plus l'avènement de l'informatique et la démultiplication des communications à travers le monde ont accéléré un processus de détermination d'un standard de chiffrement sécurisé. C'est dans ce contexte, que le 15 mai 1973 le NBS (National Bureau of Standards, aujourd'hui appelé NIST - National Institute of Standards and Technology) a lancé un appel dans le Federal Register (l'équivalent aux États-Unis du Journal Officiel en France) pour la création d'un algorithme de chiffrement répondant aux critères suivants :
- Le seul secret doit être la clef, et non l'algorithme.
- La clef doit à la fois servir au chiffrement et au déchiffrement.
- Il doit être compréhensible.
- Il doit être économique et adaptable.
- Il doit être efficace, rapide et exportable.
Plusieurs algorithmes ont alors été présentés, mais aucun d'entre eux n'a satisfait la NSA et le NBS. C'est alors, après la nouvelle publication de l'appel le 27 août 1974, que l'entreprise IBM présenta un algorithme considéré comme acceptable auprès des agences américaines. Il s'agit de l'algorithme nommé Lucifer.
Dans le but de valider sa solidité face aux attaques, la NSA s'empara de l'algorithme et le modifia. Elle diminua la longueur de la clef, la ramenant de 112 bits a 56 bits et modifia les S-box qui le constituent. De nombreuses et diverses critiques ont été reçues, notamment sur la taille de la clef, qui a été raccourcie, et les mystérieuses S-box. On soupçonnait que l'agence d'espionnage avait secrètement affaibli l'algorithme afin qu'ils (mais personne d'autre) puissent facilement lire les messages chiffrés. Malgré ces suppositions, l'algorithme a su se montrer efficace et sécurisé, jusqu'à ce que la taille de clef soit un problème du fait de la puissance de calcul des ordinateurs modernes.
Quoi qu'il en soit, le DES a finalement été approuvé en novembre 1976 et défini en tant que norme FIPS (Federal Information Processing Standard - En gros, une norme de chiffrement).
Fonctionnement
Le DES est un algorithme de chiffrement symétrique par bloc de 64 bits, basé sur un schéma de Feistel et prenant en paramètre une clef de 64 bits (Oui j'ai dit plus haut 56 bits, car dans la réalité on lui associe une clef de 64 bits dont seulement 56 sont utiles au chiffrement, les 8 bits restants servent à des calculs de parité, non évoqués dans cet article).
Pour résumé voici les grandes étapes :
- Fractionner le texte en blocs de 64 bits (8 octets) ;
- Permutation initiale des blocs ;
- Découpage des blocs en deux parties : gauche et droite, nommées G et D ;
- Étapes de permutation et de substitution répétées 16 fois (appelées rondes) ;
- Concaténation des parties gauche et droite
- Permutation initiale inverse.
Voici, pour les impatients, un schéma rapide qui résume grossièrement le fonctionnement du DES :
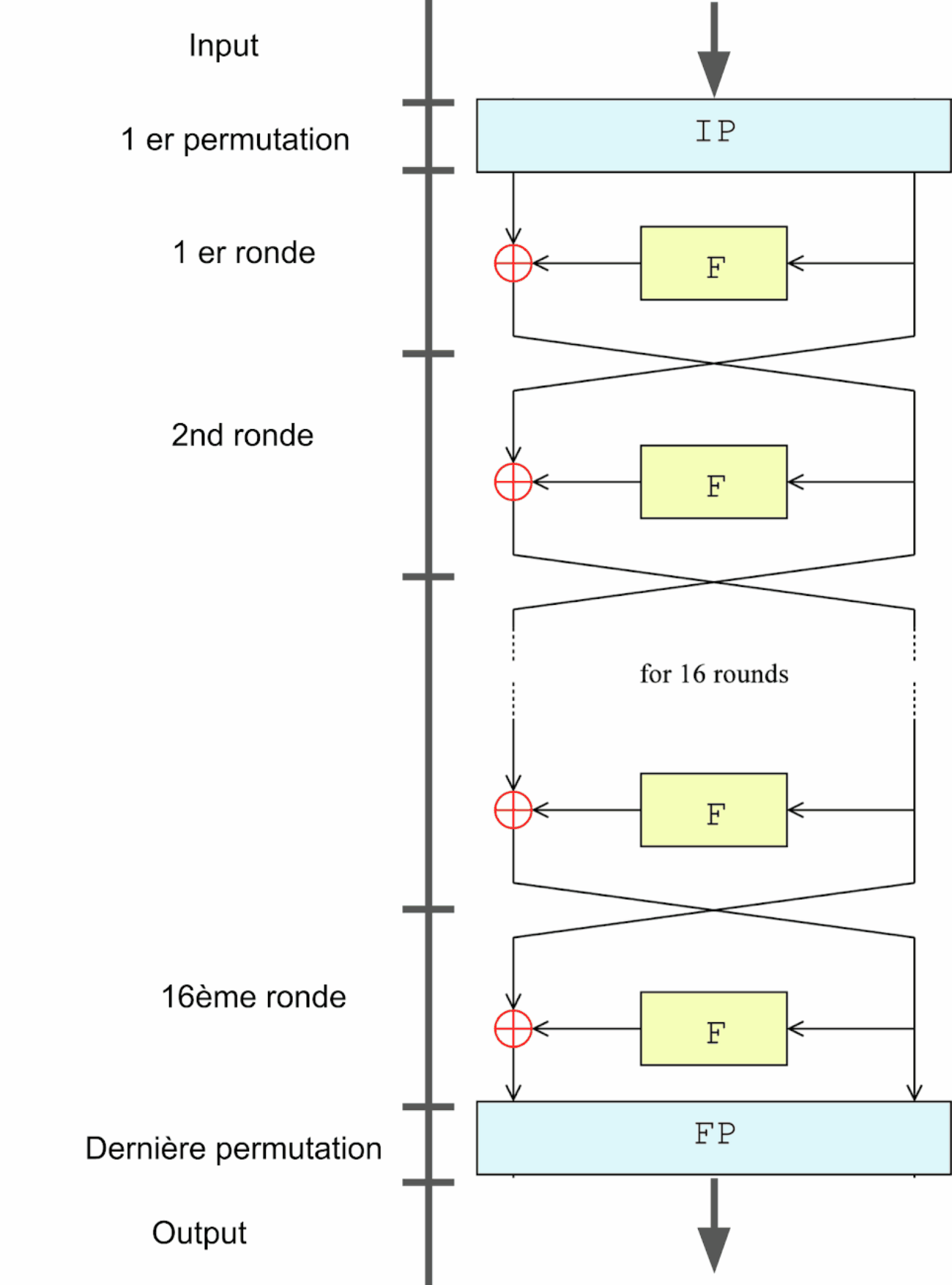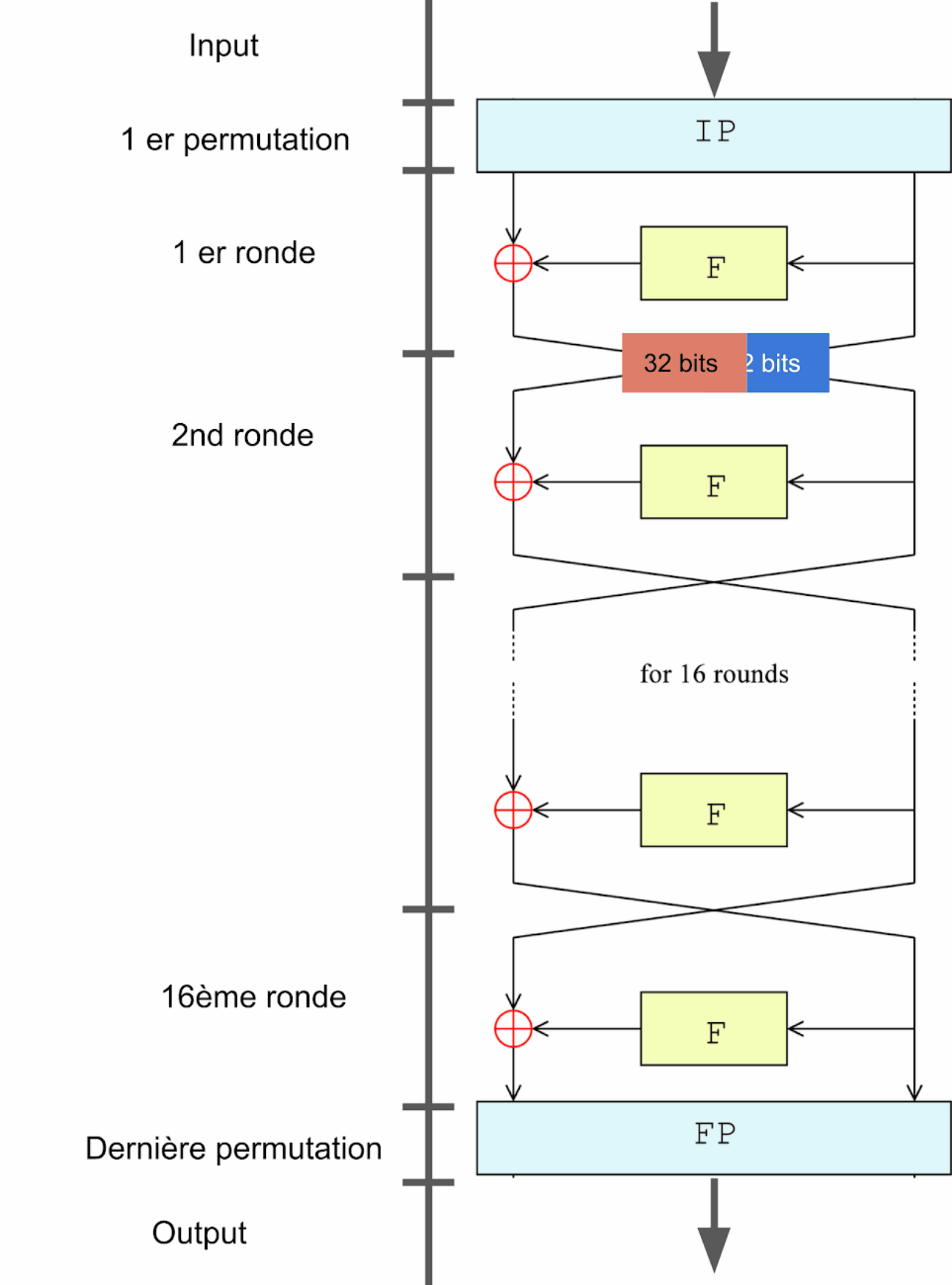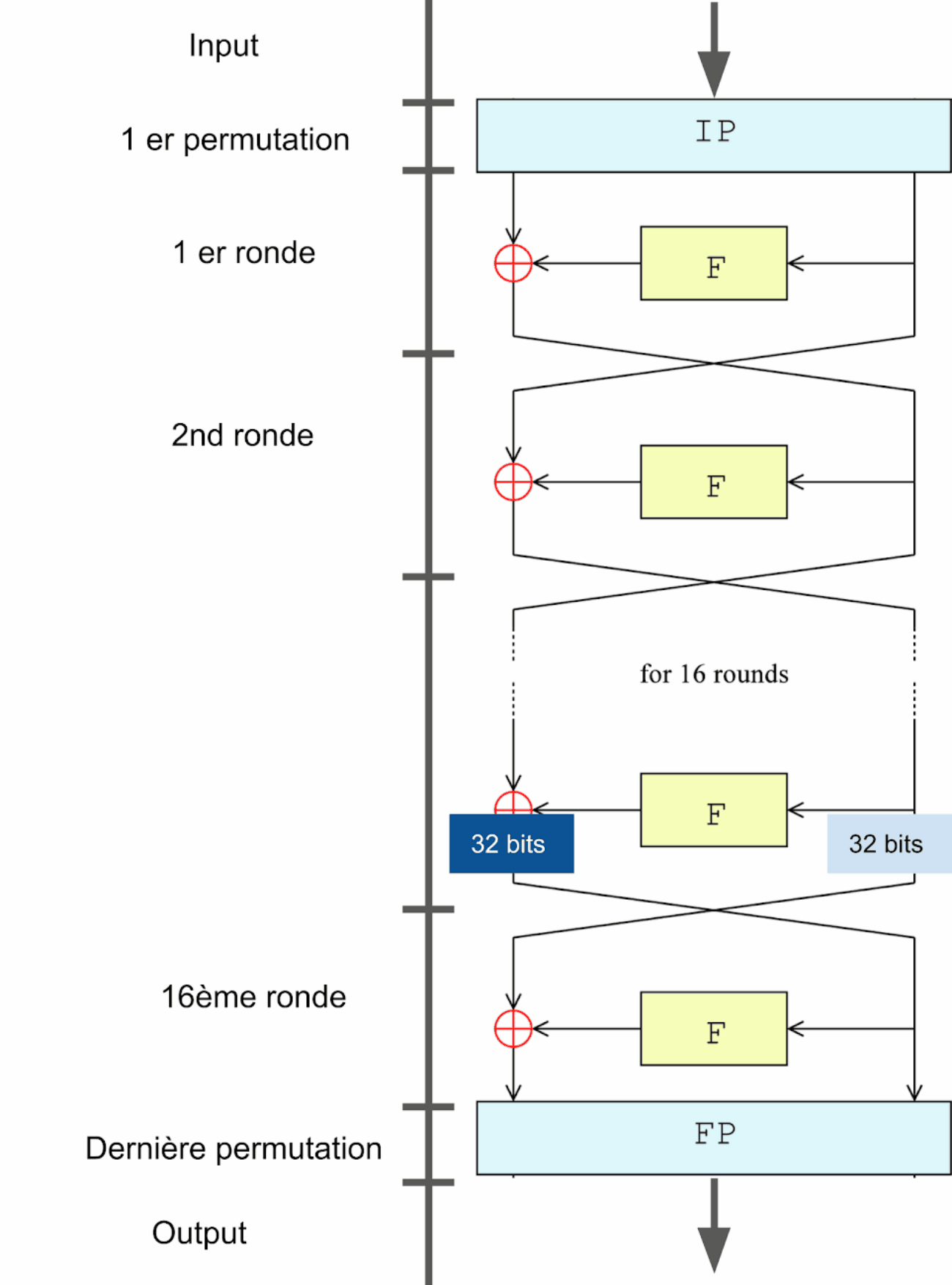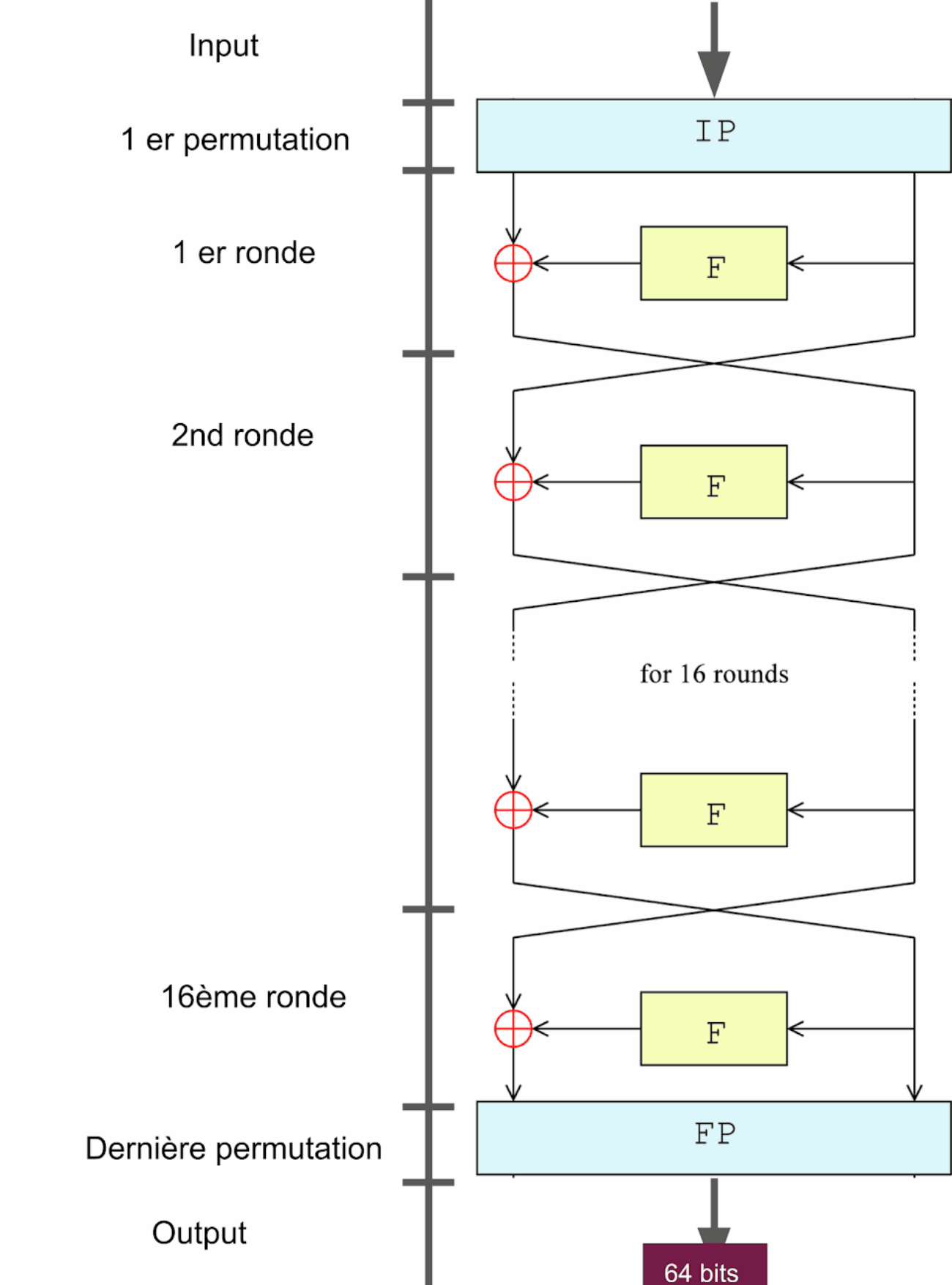
Permutation initiale des blocs
La première étape est de prendre les 64 bits du bloc à chiffrer et effectuer les permutations définies dans le tableau suivant :
| PI |
|
|---|
Ce tableau peut être vu comme une matrice de permutation qui va effectuer des permutations sur chaque bit du bloc. Dans notre cas, on peut comprendre que le 58ème bit du bloc à chiffrer arrive en première position, que le 50ème arrive en seconde position, et que le dernier bit du bloc une fois permuté était le 7ème bit du bloc d'origine.
Découpage des blocs en deux parties
Maintenant que la permutation est réalisée nous allons commencer le schéma de Feistel, en divisant le bloc de 64 bits en deux blocs de 32 bits, notés respectivement G et D (pour gauche et droite, la notation anglo-saxonne étant L et R pour Left and Right). On note G0 et D0 l'état initial de ces deux blocs. Cette division se fait à travers les matrices suivantes :
| G0 |
|
|---|
| D0 |
|
Fait intéressant : on peut remarquer que la séparation des deux blocs a été faite en fonction de la parité de la position. En effet, tous les bits ayant une position paire se retrouvent dans la branche de gauche, alors que les positions impaires se retrouvent sur celle de droite.
Les rondes
Les rondes ou rounds en anglais, au nombre de 16, vont permettre de brouiller la donnée, par le biais de 4 étapes :
- Une fonction d'expansion : Noté E
- Un OU exclusif ( XOR ) : Noté +
- Une fonction de compression (ou substitution) : Noté S
- Un second OU exclusif ( XOR ) : Noté +
En voici une représentation.
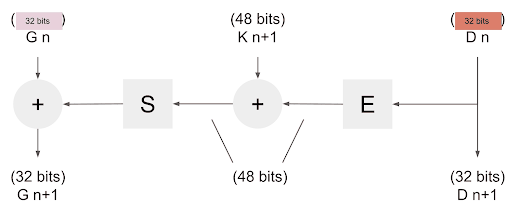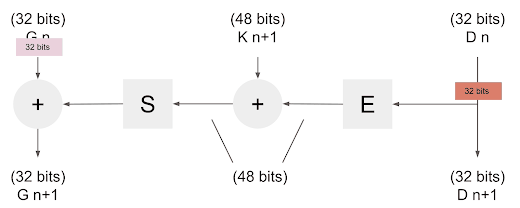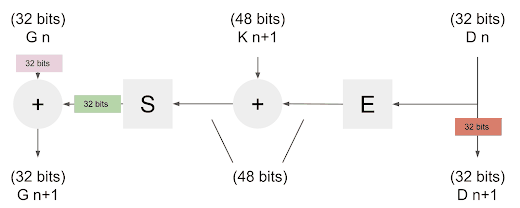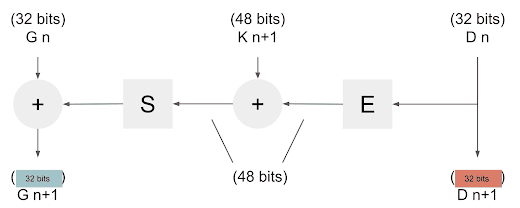
La donnée arrive par la droite (32 bits) qui entre ensuite dans la fonction d'extension, qui fait passer la donnée de 32 a 48 bits, elle est ensuite Xoré avec la clef temporaire (nous verrons cela plus tard). Elle poursuit son chemin dans la fonction de compression qui va à nouveau faire passer la donnée de 48 à 32 bits, avant d'être Xoré avec la donnée de gauche pour finir la ronde.
Fonction d'expansion
Première action de la ronde, cette fonction prend en entrée un bloc de 32 bits et ressort un bloc de 48 bits. Pour arriver à ce résultat, la fonction va suivre une matrice d'expansion (appelée table d'expansion E), qui va intervertir des bits et en dupliquer certains :
| E |
|
|---|
Ainsi en suivant la même logique que précédemment, le 32ème bit du bloc entrant devient le premier, le premier devient second, etc ... . Nous remarquons que les bits 1, 4, 5, 8, 9, 12, 13, 16, 17, 20, 21, 24, 25, 28, 29 et 32 sont dubliqués en gras sur cette matrice.
Fonction OU exclusif ( XOR )
Il résulte donc de la fonction d'expansion une chaîne de 48 bits qui va être Xoré avec la clef temporaire. Nous verrons plus tard pourquoi, temporaire, et comment elle est générée, tout ce qu'il faut retenir, c'est que cette clef fera toujours 48 bits.
Petit rappel de la table de vérité d'un XOR
| A | B | A xor B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Fonction de compression
La fonction de compression ou S-box (oui, ce sont les fameux objets vus dans la partie Histoire que la NSA a modifié, sans trop d'explications), est une fonction qui va transformer les 48 bits d'entrée en 32 bits à la sortie. Pour ce faire elle ne va pas utiliser une, ni deux, ni trois, mais ... huit matrices de substitution ! Le bloc d'entrée (48 bits) va être divisé en 8 blocs de 6 bits, et à chaque bloc sera associé une S-box, respectivement le premier bloc aura la première S-box (S1), le second la seconde (S2), etc jusqu'au 8ème bloc qui aura S8.
Voici la première fonction de substitution, représentée par une matrice de 4 par 16 :
| S1 |
|
|---|
Puis pour trouver les bits associés à travers cette matrice nous utilisons nos 6 bits (trouvés précédemment), le premier et le dernier définirons la ligne a utiliser sur la matrice et les quatre bits restants (2, 3, 4, 5) identifierons la colonne à utiliser. Le résultat sera l'intersection en binaire de la ligne et de la colonne précédemment trouvées.
Un exemple est le bienvenu :
Après avoir divisé mon bloc d'entrée de 48 bits en 8 blocs de 6 bits, je récupère le premier bloc : 101000.
- Je récupère le premier et le dernier bit : 1,0
- Je regarde l'équivalent de 10 en base 10, c'est 2.
- Donc ma ligne sera la 3ème (numérotée 2)
- Je récupère les 4 bits non utilisés : 0100
- Je regarde l'équivalent de 0100 en base 10, c'est 4.
- Donc ma colonne sera la 5ème colonne (numérotée 4)
- Je cherche l'intersection entre la 3ème ligne et la 5ème colonne : 13
- Je retourne l'équivalent de 13 en binaire : 1101
Et pour le plaisir de vos yeux voici les 7 autres S-box:
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
De chaque bloc, il ressort un ensemble de 4 bits, ce qui formera donc bien un nouveau bloc de 32 bits.
Seconde fonction OU exclusif ( XOR )
Une nouvelle fois, un Xor va être effectué. Mais cette fois entre les 32 bits de la branche de droite (voir le schéma ci-dessus) et le résultat de la fonction précédente (S-box). Une fois ce Xor effectué le tour de ronde est fini. Pour rappel, cette ronde est effectuée 16 fois.
Permutation final des blocs
Une fois les 16 rondes effectuées, les blocs de gauche (G16) et droite (D14) sont recollés par la matrice suivante :
| PI-1 |
|
|---|
Et si tout va bien nous voici à nouveau avec un bloc de 64 bits, mais chiffré via DES !
Génération des clef DES
Et oui comme tu as pu le voir dans le titre, ou le comprendre plus haut, il n'y a pas qu'une seule clef, mais plutôt 16. Mais ces 16 clefs sont dérivées d'une seule et même clef, et devines quoi ? C'est encore et toujours grâce à des matrices de permutations ! Voici comment ça se passe !
Comme on l'a vu au début, dans les 64 bits de clef de chiffrement seulement 56 sont utilisés :
| CP-1 |
|
|---|
Et comme le montre cette matrice de permutation les bits multiples de 8 ne sont pas utilisés (8, 16, 24, 32, 40, 48, 56, 64), et pour les yeux les plus experts, vous remarquerez qu'il n'y a pas un tableau, mais deux. En effet, la prochaine étape est de séparer le bloc de 56 bits (ci-dessus) en deux blocs composés de 28 bits :
| Gauche |
|
|---|
| Droite |
|
|---|
Chaque moitié de clef subit une rotation à gauche d'un bit aux étapes 1, 2, 9, 16 et deux bits aux autres étapes.

Puis on en ressort une clef de 48 bits en concaténant les deux blocs et en leur appliquant cette dernière permutation :
| CP-2 |
|
|---|
Si tout va bien nous aurons pour chacune des 16 étapes une clef de chiffrement pour la ronde associée.
Conclusion
Et voici donc le fonctionnement de cet algorithme emblématique de la fin du XXème siècle. Déprécié à ce jour, du fait de sa clef de trop petite taille, il ne doit plus être utilisé tel quel pour assurer la confidentialité des messages. Mais son fonctionnement n'en reste pas moins intéressant. En effet, le schéma de Feistel qui le compose, a été moulte fois cryptanalysés, mais jamais vraiment "cassé" proprement parlant, des attaques de type cryptanalyse linéaire/différentielle, ont réussi à éprouver quelques faiblesses, mais sur des versions affaiblies du schéma (avec moins de tours).
Si l'on parle des attaques sur le DES, d'un point de vue général, c'est la même chose que pour son schéma de Feistel, les meilleures cryptanalyses sont basées sur des attaques de type cryptanalyse linéaire/différentielle, mais toujours sur des versions affaiblies du DES, sa vraie faiblesse réside donc bien et uniquement en la taille de sa clef.
Aujourd'hui, avec la puissance des ordinateurs modernes, du cloud et de la parallélisation, une clef DES peut être cassée en moins d'une journée. Augmenter la taille de clef semble donc être la solution, mais en vain. Des propositions d'amélioration du DES avec des clefs plus grandes ont été faites, mais à chaque fois il en découlait un affaiblissement de l'algorithme. Seule solution, enchaîner deux, voir trois, chiffrements DES à la suite ?
le 25 fév. 2026 15:25
0 Commentaire
Il n'y a pas encore de commentaire. Sois le premier à en déposer un !