2DES, pourquoi pas ?
Précédemment nous avons vu le fonctionnement du DES, et avons observé que sa principale faiblesse, à l'heure actuelle, réside en la taille de sa clef. En effet, par défaut les clefs du DES ont une taille de 64 bits dont seulement 56 sont utiles (cf Le fonctionnement du DES). Mais comme le préconise le RGS (Référentiel général de sécurité proposé par l'ANSSI, c'est un document qui indique les bonnes pratiques en terme de sécurité informatique), la taille minimale des clefs pour un algorithme de chiffrement symétrique devra être, au moins, de 128 bits après 2020. Une idée possible serait donc d'enchaîner deux chiffrements DES avec des clefs différentes. Cet agglomérat de chiffrements mettrait donc en jeu deux clefs de 64 bits qui seraient équivalentes à une clef de 128 bits comme le recommande l'ANSSI. Mais nous allons voir pourquoi cette idée n'est pas restée très longtemps dans la tête de nos amis les cryptographes.
Le 2DES techniquement, c'est quoi ?
Tout est dit dans le nom le 2DES ou double DES c'est simplement le fait d’enchaîner deux DES d'affilés pour chiffrer un même bloc.
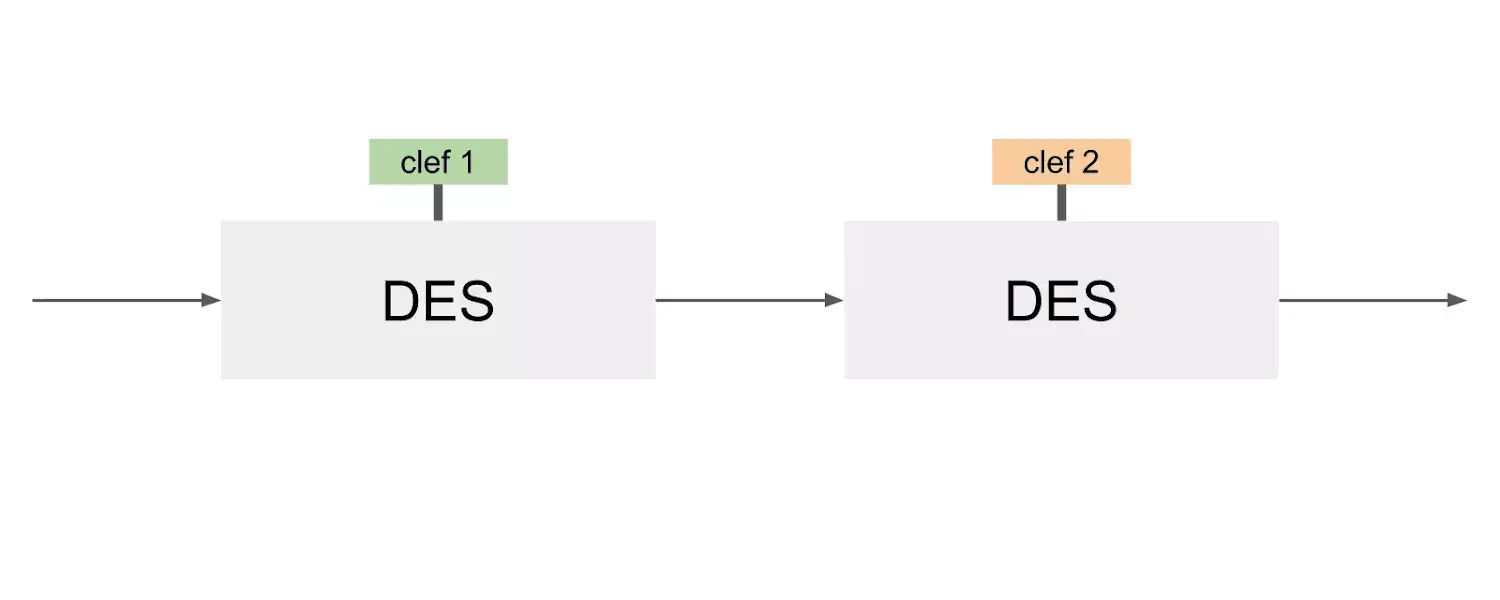
Cela peut vous paraître être de l'arnaque, mais, si on représente, cet enchaînement comme une brique élémentaire, nous aurons notre petit nouveau 2DES avec une clef de 128 bits.
Pour rester dans le contexte, l'ancienne clef de 64 bits pouvait être cassée en un peu plus d'une journée, mais là, avec ses 128 bits, casser cette clef par la force brute (c'est-à-dire tester toutes les combinaisons de clefs possibles), il faudrait environ quelques milliards d'années, à quelques jours près 😂. Mais bien sûr, ce temps astronomique reste en fonction de la puissance des ordinateurs actuels. Autant dire que se lancer dans une telle attaque est une perte de temps, sauf si vous avez quelques milliards d'années devant vous à combler.
De plus, on a vu que la seule vraie faiblesse du simple DES était la taille de sa clef, ici nous avons deux DES, donc aucune autre attaque connue, mise à part la taille de sa clef qui, dans notre nouveau cas, a été doublée et donc n'est plus un problème. Le voilà l'algorithme de cryptographie parfait !
Mais il y a un hic. Si c'est si parfait et que la taille de clef est celle recommandée, pourquoi on ne le voit nul part ? C'est parce qu'en cryptographie, même si une brique est étanche, deux briques ensemble, ne le sont pas forcément. Un empilement de briques peut aussi bien faire une maison dans laquelle on peut s'abriter, qu'un tas de gravats que l'on veut se débarrasser. Cet objet en est la parfaite représentation.
L'attaque !
Comme vous vous en doutez, si on ne voit jamais cet algorithme, c'est qu'il existe une attaque (ou plusieurs), autre que la force brute qui met à mal notre sujet. J'ai nommé : meet-in-middle (attaque par le milieu, ou rencontre au milieu, en français). Cette attaque ne va pas permettre de déchiffrer n'importe quel texte chiffré via le 2DES, mais va trouver la clef utilisée entre un texte en clair et son équivalent chiffré.
Étape 1 : Création d'un bloc à casser :
Pour cela, on s'autorise à avoir un oracle de chiffrement, c'est-à-dire un objet, une personne, un service qui va pouvoir te chiffrer ce que tu lui donnes.
À savoir que cet oracle n'est pas rare. Dans la vie réelle, on peut souvent retrouver cet oracle en écoutant simplement le réseau. En effet, tous les protocoles réseaux sont normés via des R.F.C ou autre donc il n'est pas difficile de prévoir des en-têtes de protocole et de retrouver son chiffré associé.
Exemple
Lorsque tu fais une requête HTTP pour afficher un site web. Le site web va te renvoyer toutes ses informations dans un format précis avec des en-têtes. Voilà un exemple de réponse serveur avec son équivalent hexadécimal:
| HTTP/1.1 200 OK | 48 54 54 50 2f 31 2e 31 20 32 30 30 20 4f 4b 20 |
Si ces données sont chiffrées par le 2DES il sera facile de trouver a quel bloc chiffré correspond le texte. Et on le sait car le 2DES chiffre uniquement des blocs de 64 bits (8 octets) en des blocs de 64 bits tout en conservant l'ordre. Ainsi on peut découper le bloc chiffré qui suit de cette manière :
| Texte chiffré | af 58 02 cf 35 30 2e 5d 85 03 73 2e ff 45 ac | |
| Découpage en bloc de 8 octets | af 58 02 cf 35 30 2e 5d | 85 03 73 2e ff 45 ac |
| Équivalence | HTTP/1.1 | 200 OK |
Et pour trouver le texte chiffré, il suffit d'écouter le réseau via des outils comme Wireshark. Et voilà nous avons bien ici un oracle, qui va pouvoir chiffrer tout ce qu'on lui donne.
PS : Cet exemple sert à illustrer l'idée, il a simplifié beaucoup de choses, mais l'idée est là et elle fonctionne.
Retour à l'attaque, nous donnons à notre oracle le clair P1 et il nous retourne le chiffré C1, nous avons donc notre couple de départ, recherchons maintenant la clef qui a été utilisée.
Étape 2 : Génération des clefs
La seconde étape consiste à générer toutes les clefs DES possibles, il y en a 264.
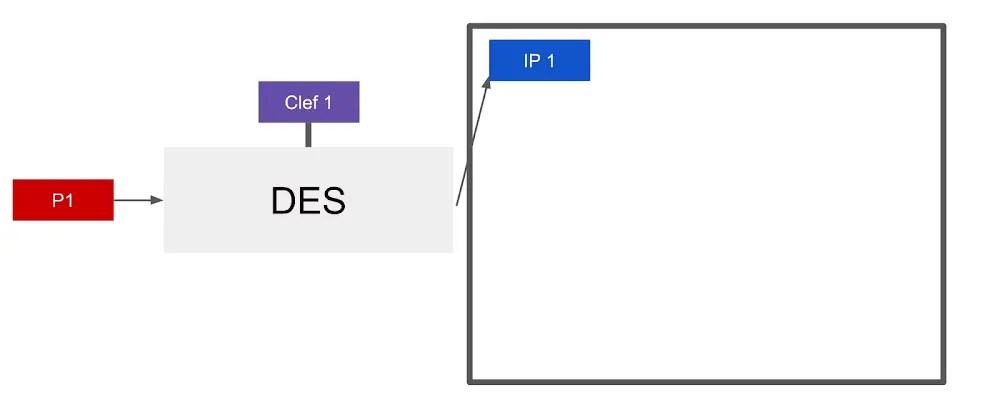
Étape 3 : Génération des chiffrés intermédiaires via P1.
Comme on l'a vu le 2DES consiste à chiffrer un texte en clair avec un DES, qui nous donne un premier chiffré (chiffré intermédiaire). Et ce chiffré intermédiaire est une nouvelle fois chiffré avec le DES et une clef différente.
Pour la suite de l'attaque, nous allons donc générer tous les chiffrés intermédiaires possibles. Pour cela, on récupère les 264 clefs de la seconde étape. Pour chaque clef, on calcule le chiffré intermédiaire grâce au texte clair P1 et la clef. On garde ensuite en mémoire, pour chaque chiffré intermédiaire trouvé, le couple (clef; chiffré intermédiaire)
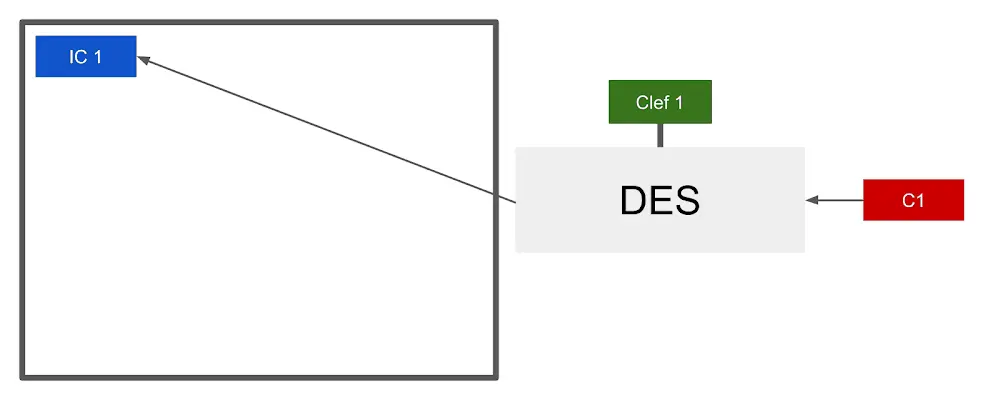
Étape 4 : Génération des chiffrés intermédiaires via C1.
Pour déchiffrer un texte chiffré en DES avec la clef "JESUISUNECLEF", il suffit de le repasser dans le DES avec la même clef. Grâce à cette idée, nous allons pouvoir générer tous les chiffrés intermédiaires qui, une fois chiffrés via le DES nous auraient donné C1.
Pour cela même logique, on récupère les 264 clefs, de la seconde étape et pour chaque clef, on trouve le chiffré généré par la clef, C1 et le DES. On garde en mémoire, ensuite pour chaque chiffré intermédiaire trouvé, le couple (clef; chiffré intermédiaire)
Étape finale : Déduction de la clef.
Nous avons donc généré deux ensembles de couple dans les étapes 3 & 4. Il suffit maintenant, de trouver les deux chiffrés intermédiaires en commun entre les deux ensembles. Et en déduire leurs clefs associées. Et voilà ! Voici la clef utilisée par le 2DES.
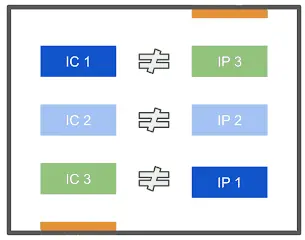
Pourquoi ça fonctionne ? Pour qu'un message soit chiffré via le 2DES; il passe forcément dans l'état chiffré intermédiaire. Vu qu'il passe dans les deux DES, il est obligé d'être un chiffré intermédiaire des deux DES. C'est pour cela que l'on a généré tous les chiffrés intermédiaires possibles et recherché celui en commun.
Conclusion
Cette attaque a cassé le DES en seulement 2 x 264 = 265 étapes (On génère deux fois l'ensemble des 264 possibilités), ce qui est quand même 263 fois plus simple que les 2128 bits de protection promis. De plus, toutes les démonstrations faite ici, ont été effectuées avec des clefs de 64 bits, mais comme vu dans l'article sur le DES, sur les 64 bits des clefs, seulement 56 bits servent effectivement au chiffrement, ce qui ramènerais donc le 2DES à une protection de 2112 bits.
Cette attaque a permis de démontrer qu'enchaîner deux DES ne donne qu'un gain d'un bit de sécurité. Mais le plus important à comprendre, c'est que cette attaque ne se limite pas au 2DES. Tout autre algorithme de chiffrement par bloc est sensible à cette attaque s'il est juste doublé. C'est pour cela que nous ne verrons jamais 2AES.
Et pour le 3DES vous allez me demander. Cette attaque ne fonctionne pas sur les algorithmes triplés d’où l'existence du 3DES, encore largement utilisé de nos jours, et qui ne connais pas, à l'heure où j’écris ces lignes, d'attaque efficace contre lui.
le 25 fév. 2026 15:26
0 Commentaire
Il n'y a pas encore de commentaire. Sois le premier à en déposer un !